Tutorial
© 2009 Kayser
last updated: July 21, 2010
 |
CSD toolbox home | |
| CSD toolbox tutorial | ||
| common mistakes and errors | ||
| frequently asked questions FAQs |
This basic tutorial assumes that the content of the CSD toolbox zip archive has been extracted to a local folder, and that this folder folder has been added to the MatLab search path (in MatLab, click on the [File] menu, and then on [Set Path...], select the folder and click on [Add with Subfolders...]). The tutorial is written on a level that is (hopefully) suitable to MatLab novices, but it does not teach the basic concepts of MatLab or the use of the MatLab environment. On the other hand, this tutorial should also be informative for experienced MatLab users who have not used the CSD toolbox. |
| Data Processing Steps | Step 1 | |
| Step 2 | ||
| Step 3 | ||
| Step 4 | ||
| Step 5 | ||
| Step 6 | ||
Step 1: Understanding Spherical Coordinates |
|||||||||
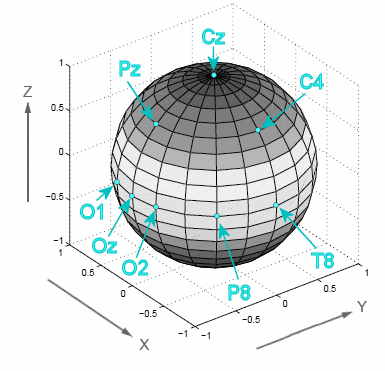
Scalp surface Laplacian estimates are based on the second spatial derivative of the recorded surface potentials and represent the magnitude of the radial (transcranial) current flow leaving (sinks) and entering (sources) the scalp. These reference-free current source density (CSD) estimates map the direction, location and intensity of current generators that underlie an EEG/ERP topography. Thus, the first step requires the identification of the scalp locations included in any given EEG/ERP topography in 3-D space. Any EEG/ERP topography is based on an EEG montage, which includes the EEG recording reference. For a spherical spline surface Laplacian, one can simplify the head as a unit sphere (i.e., a sphere with a radius of 1; Fig. 1), with all EEG scalp sites located on the sphere's surface (Fig. 2).
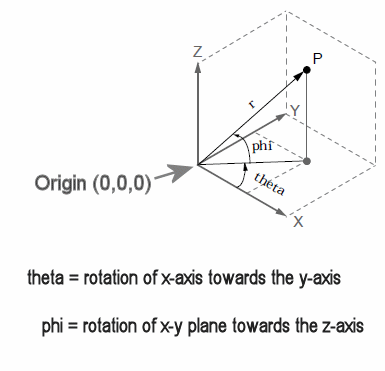
Their surface locations can then be expressed by the direction of a vector originating in the center of the sphere (Fig. 3).
Whereas the assignment for the axes and angles is arbitrary, the CSD toolbox uses the following orientations (as defined in the appendix of Kayser & Tenke, 2006a): For Cartesian coordinates, the x-y plane is marked by the great circle combining the locations Fpz, T7, Oz, and T8, with the x-axis running through T7 (-1.0) and T8 (+1.0), the y-axis running through Oz (-1.0) and Fpz (+1.0), and the z-axis running through the origin of the x-y plane (0) and Cz (+1.0). For spherical coordinates, the angle theta denotes the rotation from the x-axis towards the y-axis (positive poles, respectively), whereas phi denotes the angular displacement from the x-y plane towards the positive pole of the z-axis. The spherical coordinates for locations where the three great circles of the x-y, x-z, and y-z planes intersect are straightforward (e.g., for Oz: theta = -90, phi = 0; for Cz: theta = 0, phi = +90; for T8: theta = 0, phi = 0). As defined by the logic of the international 10-20 system (e.g., Oostenveld & Praamstra, 2001), intermediate locations on these great circles are quarter (22.5°) or quintile (18.0°) sections of the respective rectangular arcs (e.g., for O1, theta is -90 - 1*18 = -108, phi = 0; for Pz, theta = -90, phi is 2 * 22.5 = +45; for P8, theta is 2 * -18 = -36, phi = 0). Similarly, locations on the small circle combining nasion and inion are a quarter rectangular arc downwards (e.g., for P10, theta is 2 * -18 = -36, phi = -22.5). The remaining locations are located on small circles defined by two lateral and one midline base locations (Oostenveld & Praamstra, 2001). Determining their spherical angles is less straightforward, but can nevertheless be derived by performing some basic geometrical computations (as detailed here). If you are using non-standard scalp locations (i.e., those not covered by Step 2, you need to fully understand this systematic and specify your spherical coordinates through Theta and Phi. For this purpose, the original publication included as an example the Matlab code GetF3CoordinatesWithMirrorLocations.m, along with two Matlab functions (SphericalMidPoint.m, LineWithSphere.m) to support these geometrical computations. |
|||||||||
| Back to top | Home | Tutorial | Errors | FAQs |
Step 2: Specifying an EEG Montage |
|||||||||||||||||
If you are using an EEG montage including only standard 10-20-system locations, you can easily specify your EEG montage by taking advantage of the CSD toolbox content. The CSD toolbox includes a look-up table for 330 standard scalp sites based on the systematic of the extended 10-20-system (10/20-, 10/10- or 10/5-system; cf. Jurcak et al., 2007; Fig. 4), plus additional locations for left and right preauricular points (A1/A2; LPA/RPA = T9/T10), left and right mastoids (LM/RM = TP9/TP10), and the nose tip (Nose). In addition, 129 scalp locations of a first-generation geodesic sensor net (GSN; Electrical Geodesics, Inc.) used in our report addressing the feasibility of a CSD transform for low-density EEG recordings (Kayser & Tenke, 2006b) have been included (Fig. 5). [However, in deviation from the original 129-channel GSN montage, the location for channel #17 points to the Nose instead of Nz; if appropriate, this location must be adjusted in the look-up table by replacing the values for channel #17 with the values for Nz.]
This look-up table is an ASCII file ("10-5-System_Mastoids_EGI129.csd"), in which each line lists a scalp location with their spherical coordinates Theta and Phi (Fig. 6). [The additional values in each line (Radius, X, Y, Z, off sphere surface) are gratuitous and provided only for backward compatibility.]
The CSD toolbox function ExtractMontage.m provides an easy means to extract a specific EEG montage from this look-up table, which is best explained via a hands-on example. Included in the CSD toolbox are the data of a grand mean ERP (ASCII file "NR-C66-trr.dat"; Fig. 7) derived from 66 healthy adults (the target condition for an auditory oddball task using complex tones with a right button press; cf. Kayser & Tenke, 2006a) along with the corresponding 31-channel EEG montage (ASCII file "E31.asc"; Fig. 8). The ERP data are stored as a "Samples × Channels" matrix, meaning each row represents a single time point (200 samples/s; 200 time points ranging from 0 to 995 ms), and each column corresponds to a scalp location (ordered from Fp1 to Nose, as given by the line-by-line EEG montage listed in file "E31.asc"). Note that all values in the last column of the ERP data matrix, which corresponds to the Nose recording site, are zero because these surface potential data are nose-referenced.
We can use the MatLab function textread.m to read the EEG montage as a cell array of strings into MatLab, by entering
at the MatLab command window (Fig. 9). You can also open the MatLab code for this hands-on example (ExampleCode1.m) in the MatLab editor, highlight line 19 and press the <F9> key. Either way, the EEG montage should now be a new cell string matrix E listed in the MatLab workspace. [Note that by entering MatLab statements at the command window prompt without a terminating semicolon (character ';'), any return value(s) of that statement will be displayed within the command window; adding a semicolon to the end of the statement will suppress this output.] Next, we use the CSD toolbox function ExtractMontage.m with the look-up table for the spherical coordinates and cell string array for the EEG montage by entering
at the MatLab command window (Fig. 10). The MatLab workspace should now list two matrices, E and M. To verify the integrity of the EEG montage, which is of crucial importance for the CSD transform, we use the CSD toolbox function MapMontage.m with the matrix M by entering
at the MatLab command window. This creates a MatLab figure showing a crude 2-D topography of the EEG montage (Fig. 11).
|
|||||||||||||||||
| Back to top | Home | Tutorial | Errors | FAQs |
Step 3: Generate Transformation Matrices G and H |
|||||||
The next step generates two "Channels × Channels" transformation matrices termed G and H in the original Perrin et al. (1989) algorithm. These transformation matrices, which are used for the spherical spline interpolation of surface potentials (G) or current source densities (H), depend only on the number and relative position of surface locations included in the EEG montage (i.e., their cosine distances). For this reason, these matrices have to be computed only once for any given EEG montage. For the same reason, the CSD transform itself depends only on spatial EEG/ERP properties (i.e., the surface potential topography present at any sample/time point), not temporal EEG/ERP properties. The computation of the G and H matrices is provided by the original published function GetCSD.m. However, because this function included a call to the actual CSD transformation function CSD.m, the separation of these steps became somewhat blurred. The new CSD toolbox function GetGH.m resolves this issue but computing only the G and H matrices for a given EEG montage M (i.e., a structure array generated by the CSD toolbox function ExtractMontage.m) by entering
at the MatLab command window (Fig. 12). Alternatively, one can highlight and evaluate (<F9>) lines 23 through 25 of ExampleCode1.m in the MatLab editor, which include the MatLab tic and toc statements, which provide the computational time for these transformations (it takes about 17 s for this 31-channel EEG montage using MatLab® R2009a running under Microsoft Widows XP with SP3 on an Intel® CoreTM 2 CPU 2.13 GHz). The MatLab workspace should now list four matrices, E, M, G and H.
In contrast to the original published function GetCSD.m, the new function GetGH.m allows the specification of the so-called m-constant, which affects the flexibility of the spherical splines. For instance, entering
will compute G and H transformation matrices of medium (G3, H3) or high (G2, H2) spline flexibility. Valid values for m are 2 to 10. The default, m = 4, causes a rigid spline interpolation, whereas m = 3 (medium) and m = 2 (most) yield more flexible splines (Fig. 13). [Using values of m > 4 will result in increasingly stiff spline interpolations, thereby changing the spatial filter properties.]
|
|||||||
| Back to top | Home | Tutorial | Errors | FAQs |
Step 4: Prepare the Input Data |
|||||||||||||||
Obviously, the surface potential data must be accessible in order to compute CSD estimates. To submit the ERP data of our example file to the CSD.m function, we use again the MatLab textread.m function by entering
at the MatLab command window, which will create a "Samples (200) × Channels (31)" double matrix D in the MatLab workspace (Fig. 14). [Note: At least in two versions of Matlab (Versions 6.5.0.180913a, June 18, 2002, and 6.5.1.199709, August 4, 2003, both Release 13), the execution of this textread.m statement incorrectly reads a "200 × 32" double matrix, that is, it falsely adds a column with zeros. In this particular case, this can easily be corrected by removing the last column, e.g. by entering "D = D (:,1:31)" at the command line. While this is clearly a MatLab implementation bug that has been fixed in more recent revisions of the software, you should always verify the dimensions of the data matrix.]
However, because CSD.m requires "Channels × Samples" input format (i.e., the channels are the matrix rows, and the samples are the matrix columns), we have to transpose the matix first by entering
at the MatLab command window (the apostrophe character is used in MatLab as the complex conjugate transpose operator), after which the MatLab workspace indicates this matrix reorientation (Fig. 15). [Note: In matrix algebra, a transpose of a matrix is created by writing the matrix rows as columns and vice versa, thereby transforming a n × m matrix to a m × n matrix.]
Similar data preparations may have to be performed for other surface potential data (e.g., single trial EEG epochs, continuous raw EEG, individual ERPs) to submit these data in a "Channels × Samples" matrix format to function CSD.m |
|||||||||||||||
| Back to top | Home | Tutorial | Errors | FAQs |
Step 5: Apply the CSD transform |
|||||||||||||||
The next step is to apply the actual CSD transform to the EEG/ERP data using the corresponding transformation matrices G and H. This computation is provided by the CSD toolbox function CSD.m, which is essentially unchanged from its original publication. We compute the CSD estimates of these ERP data by entering
at the MatLab command window (it takes about 1/10th s to convert these these 200-samples, 31-channel ERPs to CSDs). To view these these CSD waveforms, we can use the Matlab figure routine plot.m. To use this routine appropriately for the CSD waveforms, we have to transpose the CSD output matrix X, which has the same "Channels × Samples" orientation as the input matrix D, to a "Samples × Channels" orientation by entering
at the MatLab command window. We can now view the CSD waveforms with the MatLab plot.m function by entering
at the MatLab command window, which will create a MatLab figure (Fig. 16). [Alternatively, we could have also entered "plot(X')" with the transpose apostrophe added to the input matrix at the command line. Note that line 34 of ExampleCode1.m opens a new MatLab figure with the statement "figure;" to avoid plotting on any existing figure; if no MatLab figure is open, the plot.m function will automatically create a new figure.] Individual channel waveforms can be compared by referencing their matrix columns. For instance, we know that scalp sites Cz and Pz must correspond to columns 14 and 24, respectively (e.g., see Fig. 10, or load data matrix E into the variable editor by double-clicking on E in the workspace). Thus, by entering
at the MatLab command window, the figure plot will compare the CSD waveforms for Cz and Pz (Fig. 17).
Note that the abscissa (x-axis) refers to the waveform data in sample rather than time points. Because these data were sampled at 200 Hz (5 ms per sample point), and the first data is zero (stimulus onset), the prominent negative deflection for site Cz at sample point 21 (Fig. 17) corresponds to a latency of 100 ms (i.e., an auditory N1 sink), and the prominent positive deflection for site Pz at sample point 73 (Fig. 17) corresponds to a latency of 360 ms (i.e., a P3 source). The data along the ordinate (y-axis) reflects CSD units, which are by default µV/m² (microvolt per square meter). After again transposing the ERP data matrix D, we can plot the corresponding ERP waveforms for comparison by entering
at the MatLab command window, which will create MatLab line graphs for ERP waveforms (Fig. 18 and Fig. 19).
Note that the ordinate (y-axis) reflects now ERP units [µV], and the zero data for the Nose reference is easily recognized (see red flat line in Fig. 18). The online documention of the CSD toolbox function CSD.m, which is displayed after entering
at the MatLab command window (Fig. 20), reveals two additional input parameters for this routine that allow to specify the λ (lambda) smoothing constant and the head radius (head).
By default, a smoothing constant of 0.00001 (1.0-5) is added to the diagonal of the G matrix. While this value is arbitrary, it is appropriate for surface potential data scaled to microvolts. Specifying a different λ smoothing constant, for instance, no smoothing by entering
or a stronger smoothing (1.0e-4 = 0.0001)
will affect the spherical spline interpolation (Fig. 21).
Specifying the head radius (head) in centimers [cm] will rescale the CSD units. By default, the unit sphere will return current source densities in microvolt/square meter [µV/m²]. By entering a more realistic head radius of 10 cm, CSD values will be returned in units of microvolt/square centimeter [µV/cm²], which simply amounts to dividing the original values by a factor of 100. [Note that a lambda value must be explicitly specified when specifiying the head radius, e.g. "X = CSD (D, G, H, 1.0e-5, 10)."] The CSD toolbox function CSD.m also allows to request the return of a surface potential matrix, which will reflect the interpolation of surface potentials from the input data after taking spline flexibility (m-constant) and smoothing (λ) into account. For a single sample point, this will be a constant value added to all scalp locations. |
|||||||||||||||
| Back to top | Home | Tutorial | Errors | FAQs |
Step 6: Save the Output Data |
|||||||
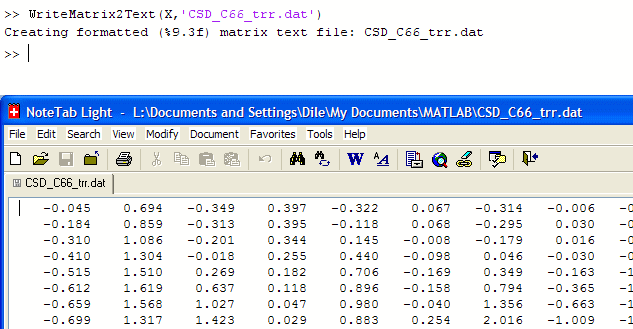
Unless the CSD output matrix is directly used by MatLab programs (e.g., when analyzing the data with EEGlab), it has to be saved for the use with other software programs. We can use the CSD toolbox function WriteMatrix2Text.m to save the CSD output matrix X as a formatted ASCII text file by entering
at the MatLab command window (Fig. 22). By default, this will use the current matrix orientation of X, which should be "Samples × Channels," to an ASCII data file, in which the rows are the samples points (200) and the columns are the scalp sites (31), with each data values written in a fixed 9-character format with 3 decimal places. [Note that without specifying a path with the ASCII file name, the output text file will be written to the MatLab working directory.]
Two additional input parameters allow the specification of a different output format and to add case numbers to each line, for instance, by entering
at the MatLab command window, the output will be written in a fixed 12-character format with 6 decimal places, including a 4-character case number at the beginning of each line (Fig. 23).
|
|||||||
| Back to top | Home | Tutorial | Errors | FAQs |
References Jurcak, V., Tsuzuki, D., Dan, I. (2007). 10/20, 10/10, and 10/5 systems revisited: their validity as relative head-surface-based positioning systems. NeuroImage, 34(4), 1600-1611. PMID: 17207640
Oostenveld, R., Praamstra, P. (2001). The five percent electrode system for high-resolution EEG and ERP measurements. Clinical Neurophysiology, 112(4), 713-719. PMID: 11275545 Perrin, F., Pernier, J., Bertrand, O., Echallier, J.F. (1989). Spherical splines for scalp potential and current density mapping. Electroencephalography and Clinical Neurophysiology, 72(2), 184-187. PMID: 2464490 [Corrigenda EEG 02274, EEG Clin. Neurophysiol. 1990, 76, 565] |
| Back to top | Home | Tutorial | Errors | FAQs |